Posted subsequent to reading David Chako's initial reports on this topic via Synergetics-L, I see this primarily as a preliminary test of my programming methods and conceptual apparatus surrounding both the 'IVM random walk' and Chako's 4-tuple v-ray-based coordinate system. [2]
METHOD
I put my IVM Turtle [3] through 5000 trials doing 100-step random walks from (0,0,0,0). Each step involves randomly choosing from 1 of 12 IVM directions. My resulting table records ordinary straight-line distances, where a segment from (0,0,0,0) to the reference tet mid-edge is defined as unity, i.e. an IVM spoke or tet edge is root8 (~2.83).[4]
I realize this is a different yardstick and distance computation from David's experiments, wherein the tetra edge is unity, but this alternative metric should not affect any underlying pattern we might find, in terms of distance distribution patterns about the origin.
HYPOTHESIS
What I expect to find (my trials are running as I write this) is
some kind of distribution around an 'average radius' for 100-step
walks. Distances closer to or further away from the origin will
taper off in likelihood, giving us a distribution curve. What this
average distance will be I'm not sure, but I'm looking for a
function like:
avgdist(100,0.5)
which will put out some range of distances (lower/upper bounds)
within which at least 50% of the walks will fall.
avgdist(100,0.2) would narrow the radial band to 20% and avgdist(100) would be some ideal average. Then we could graph avgdist(x) where x=number of steps in a random walk, maybe even come up with some algebraic rule.
RESULTS
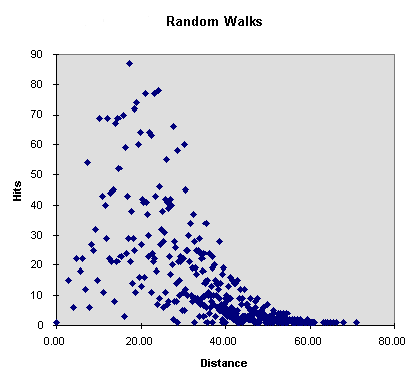 |
Average distance: 25.88 Distance attained most often: 17.20 (87 hits) Mininum distance: 0.00 ( 1 hit) Maximum distance: 71.05 ( 1 hit)
CONCLUSIONS
I guess I'm not seeing anything striking or unusual -- looks like a statistical distribution we might expect. But I'm not using huge numbers and may not have a fine precision enough approach to pick up relevant patterns. I don't have any expression for avgdist yet -- more trials required.
FURTHER THOUGHTS
Since we're confining positions to IVM sphere centers, many real number distances from the origin will never occur. Graphed against positive real distances, the pattern will always appear 'spikey' simply because the turtle is hitting a small subset of the potential radii.
Of course the frequency of the IVM relative to our unit-length is going to determine whether we see this atomic discreteness. In the case of a high frequency IVM, the distribution may be so fine-grained as to appear smooth (grains of sand are any distance you require, provided your ruler isn't too finely calibrated).
How this work relates to diffusion patterns within an ideal gas remains open to speculation. A numbering scheme along the lines of Pascal's Tetrahedron which gives a probability distribution for randomly falling balls within an IVM tetrahedron would provide some additional insights into the empirical results and perhaps facilitate a priori confirmation of our avgdist function.
EXHIBIT
Some of the code:
procedure randstudy
lparameters iter
oTurtle=CREATEOBJECT("ivmTurtle")
local k
use randbase
for k = 1 to iter && iter set to 5000 for this write-up
do randomwalk
append blank && adding a record to trials table
* e parameter says which edge in reference system is unity
replace iterno with k, distance with oTurtle.saypos("e")
endfor
release oTurtle
use
return
procedure randomwalk
=rand(-1) && seed the generator
oTurtle.setorigin()
for i=1 to 100
ivmdir = mod(int(1+1000*rand()),12)+1 && between 1 & 12
oTurtle.vemov(ivmdir)
endfor
return
ENDNOTES
[1] IVM = isotropic vector matrix -- lattice connecting sphere centers in an fcc packing.
[2] A reference tetrahedron body-centered at the origin defines two sets of rays: 4 'v-rays' from origin to vertices and 6 'e-rays' to mid-edges. The XYZ coordinate addressing scheme is based on e-rays whereas Chako's scheme uses 4-tuples (1,0,0,0)(0,1,0,0)(0,0,1,0)(0,0,0,1) to identify the v-rays, which may be scaled and summed positively to specify any point in space. For converting back and forth to/from XYZ, the following conventions are used:
v1 = ( 1, 0, 0, 0) = ( 1, 1, 1) = e1 + e3 + e5 v2 = ( 0, 1, 0, 0) = ( 1,-1,-1) = e1 + e4 + e6 v3 = ( 0, 0, 1, 0) = (-1, 1,-1) = e2 + e3 + e6 v4 = ( 0, 0, 0, 1) = (-1,-1, 1) = e2 + e4 + e5 where: e1 = +x e2 = -x e3 = +y e4 = -y e5 = +z e6 = -z
According to this scheme, the 12 directions from any IVM sphere center to neighboring sphere center are specified as:
(2,0,1,1)(2,1,0,1)(2,1,1,0) (0,2,1,1)(1,2,0,1)(1,2,1,0) (0,1,2,1)(1,0,2,1)(1,1,2,0) (0,1,1,2)(1,0,1,2)(1,1,0,2)
Since this paper was first published to the web in January,
1997, I have altered my strategy for converting to and from
Cartesian coordinates and now use the following identities:
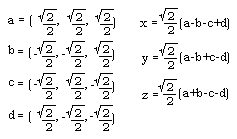
For a more detailed introduction to this topic, see my more recent
Introduction to Quadrays.
| [3] Named for Seymour Papert's kid-friendly Logo language, wherein the 4D Turtle is a draw-cursor. The turtle used for these trials is a Microsoft Visual FoxPro class defined to understand both e-ray and v-ray move instructions. The ivmTurtle subclass registers the 12 IVM directions by index number in order to facilitate randomization. Previously published IVM Turtle methods output to VRML, i.e. if your browser supports embedded VRML you'll see the 1000 step random IVM walk at right. |
|
[4] The center-to-midedge segment is likewise half the edge of a cube inside of which the reference tetrahedron is inscribed (as face diagonals). A cube with an edge of 2e has face diagonals of e * root8, which is our reference tetrahedron (e=1). The reference tetrahedron is volumetric unity as given by Gerald de Jong's modification of Euler's expression deriving any tetrahedron's volume from its 6 edges, what he calls his Sublimation Theorem (requires a Java-enabled browser).
Synergetics on the
Web
maintained by Kirby Urner