Microarchitecture of the Virus
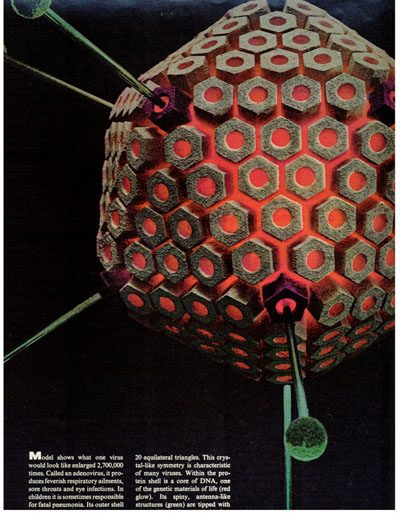
LIFE Magazine, February 1966, pg. 56
Sphere Packing and Capsomere Counts
Sometime in the 1960s virologists first
approached Fuller with a puzzle: new x-ray diffraction patterns
revealed that
many viruses were similar in structure to geodesic domes. The
protein sheaths housing the RNA were 5-fold symmetric, icosahedral
structures, and the number of capsomeres numbered 12, 42, 92...
Virologists wondered whether Fuller recognized these numbers from
his explorations with geodesic domes. He answered with his
sphere-packing formula for the number of spheres in the outer layer
of an expanding cuboctahedral packing:

[ku] 5-frequency
Given that the jitterbug transformation turns a cuboctahedral layer into an icosahedral one, the geometric basis for the number of viral capsomeres was clear. However, other common capsomere counts were not accounted for by the cuboctahedral numbers, as when the capsomeres 'wrap' around an icosahedron in a skewed pattern. Virologists Casper and Klug derived a formula that fit even more of the data, which they subsequently connected back to the geometric investigations of Michael Goldberg, a mathematician.
When Dr. Robert Horne wrote a groundbreaking article for Scientific American about these matters, he chose not to credit Fuller for having discovered anything new, although students of synergetics (including Michael Goldberg) realized at the time that Fuller's pioneering investigations, like Goldberg's, also derived from more generalized principles -- in Fuller's case these were generalizations about sphere packing in a variety of conformations, not just the cuboctahedral.
Armed with Goldberg's 1937 paper, virologists felt they were off the hook vis-a-vis hard-wiring anything from Fuller's synergetic geometry into their discipline. Many felt relieved because Fuller, something of a maverick (regarded as such even by architects), and without the academic credentials expected of a scientist, might only serve to undermine the status quo if admitted into the literature as a recognized contributor in such professional circles. The idea that virology might also serve as a useful access point leading to a more generic synergetics- informed curriculum, linking in turn to many other disciplines, at the time seemed quasi-irrelevant, if not downright alien, to these rather narrowly focused specialists.
With the subsequent discovery of a new allotrope
of carbon in the 1980s, again showing five-fold symmetric
icosaspherical geometry (variably frequenced hexa-pents), the
opportunity to provide a useful curriculum access point to
synergetics again arose. This time, by naming the newly discovered
The Scientific American has subsequently published an article about synergetics and five-fold symmetry in its Japanese edition (dinosaurs on the cover), focusing on Yasushi Kajikawa's modular decompositions of well-known five-fold symmetric shapes (e.g. the icosahedron). It's cover story in January, 1998 was also devoted to a central synergetics theme, tensegrity (as a structural principle for better understanding cell structure), which concept likewise belongs to Ken Snelson.
More relevant to the this virus thread than tensegrity, however, was a story in the previous issue (December, 1997) about metal atoms clustering in icosahedral and cuboctahedral conformations -- no link to Fuller's groundbreaking sphere-packing studies was included, even in the notes section.
For further reading:- From Platonic
bodies to geodesic spheres, fullerenes, and virus
by Dr. Karl-Dietrich Neubert - Principles of Virus Architecture
- A Case of Deja Vu in The Invention Behind the Inventions: Synergetics in the 1990s
- Synergetic Crystallography 101
- Related blog post Nov 20, 2005
Synergetics on the
Web
maintained by Kirby Urner