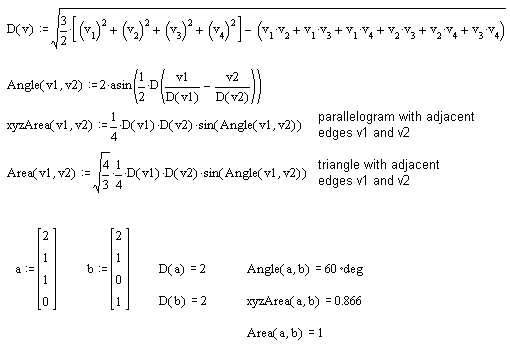Quadrays and Area
by Kirby Urner
First posted: December 26, 1997
Last updated: August 4, 1999
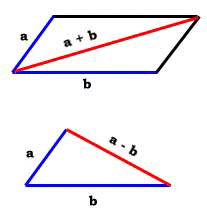
In the xyz game of vectors, the area defined by two vectors
is obtained from a parallelogram. Vectors a and b
comprise adjacent edges, while the vector
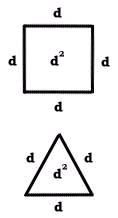
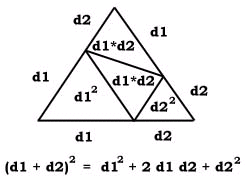
If a and b have the same length d and the angle between them is 90 degrees, then our parallelogram is a square and its area is defined as d x d or "d squared".
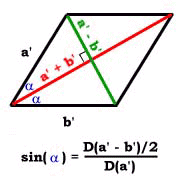
The game of quadrays includes xyz area among its library of methods but defaults to a different conceptualization of the process for deriving area from two vectors.