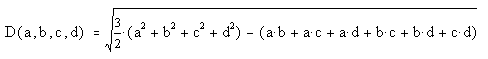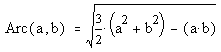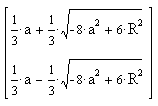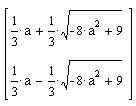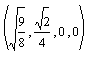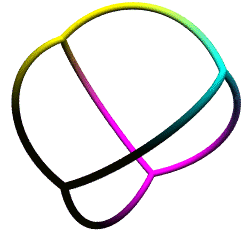Color Coordinated Quadrays
Concept by Josef Hasslberger
Execution by Kirby Urner
A work in progress
Version: 0.61
First Posted: October 12, 1997
Last Revised: December 8, 1998
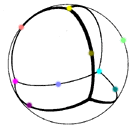
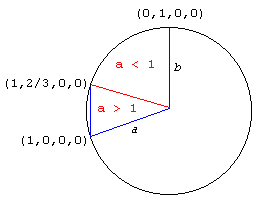
Another game with quadrays involves mapping between quadray
coordinates and colors in the Cyan Magenta Yellow Black color
specification (CYMK).
CYMK is the four-color standard used in the printing industry,
wherein colors reach the eye by light reflecting from paper. On the
computer screen, on the other hand, we work with transmitted light
using the Red Green Blue standard (RGB).
Our goal is to come up with a unit radius sphere whereon each
pixel is a of a color determined by its (c,y,m,k) coordinates,
translated to RGB for display purposes, and realizing that in each
quadrant, one of these primary colors will be set to zero.

Whereas converting to and from CYMK is a difficult process when
true color matching is sought, for mathematical purposes, a mapping
to RGB is not that difficult. The above figure shows quadrays from
the tetrahedron's center in the four primary colors, with the edges
colored using simple linear interpolation, meaning an
average of the colors at the two vertices was determined.
The RGB values for the four colors, Cyan, Yellow, Magenta and
Black are given below:
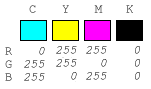
We compute the average of two primary colors by noticing which
of the RGB components change going from one vertex to another, and
pick a half way level of 128 for those components. In the chart
below, the middle column shows the color obtained by averaging the
two primary colors on either side: