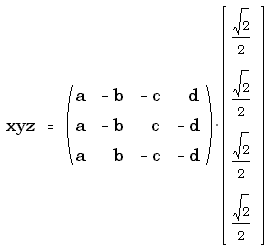Quadrays and XYZ

We can formalize the relationship between quadray and xyz coordinates by adopting conventions of both relative scale and orientation. Once these relationships have been specified, algorithms for between these two schemes may then be spelled out in detail.

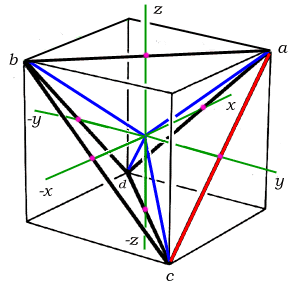
When it comes to scale, we have previously defined a logical set of edge lengths which uses the primitive, unit-volume regular tetrahedron of the synergetics concentric hierarchy as the outer frame, with the four basis radials (three of them shown at right, in blue) congruent to A module edges running from the tetrahedron's center of gravity to its four vertices.

Since this primitive tetrahedron is formed by the centers of four closest packed unit-radius spheres, we have six edges of length 2.

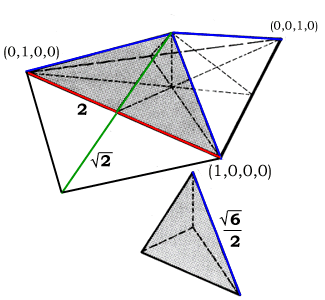
On the orientation front, we have several options as to how we choose to embed the primitive tetrahedron in an xyz cube with face diagonals of length 2. In the diagram below, an orientation was chosen such that quadray (1,0,0,0) would have all positive xyz coordinates.

Regarding the figure at left, note that although the positive x axis points away from the viewer, this is just a slightly unconventional angle on the standard left-handed xyz coordinate system used in all text books. The lettering of the quadrays is as one would expect: a = (1,0,0,0), b = (0,1,0,0), c = (0,0,1,0), d = (0,0,0,1).

The xyz-oriented green edges each protrude through respective cube face centers to opposite corners of a rhombus, the same one depicted above, with a short diagonal of root(2) and a long diagonal of 2. These edges and the edges of the cube-inscribed quadray tetrahedron bisect one another, at a distance root(2)/2 from the origin.

We are now ready to formalize the conversion algorithms. When going from quadrays to xyz, our process is to take account of how much a given quadray contributes in the x, y and/or z directions, either positively or negatively. For example, quadray a positively contributes root(2)/2 in all three directions. Once we account for each quadray's impact on the xyz economy, we end up with a set of equations. These may be efficiently expressed in matrix notation as shown at right.

Going in the other direction, from xyz to quadrays, is only a little more complicated. As before, we assess the impact of each x, y or z amount on the quadray economy. Note, however, that whereas positive x contributes to both the a and b quadrays, negative x has no impact on these two, but on c and d instead. Since quadrays use only positive numbers, a negative xyz coordinate still has a positive effect. So our matrix includes a test as to whether a given coordinate is positive (or zero) and distributes the effects to the relevant quadrays accordingly.

We're still not done however as the above matrix does not guarantee our quadray coordinates will be in simplest form, meaning with a least one zero coordinate and no negative coordinates. We can achieve this last simplification by sorting the output column in ascending order and taking the smallest term (possibly negative) off the top. By subtracting this smallest term from all elements (an identity operation in quadray space), we will reduce our quadray coordinates to their proper form.

Note that the above notation assumes matrix indexing starting at (0,0) i.e. we are column-sorting (csort) on Q's the zeroth (only) column and then taking the top-most term (zeroth row, zeroth column).

As an alternative to these matrix expressions, we can provide the same computations in a more procedural form, using computer language conventions, matrices being nothing more than fancy typography for indexed 2-dimensional arrays after all.

For converting quadrays to xyz, we might write something like:

    procedure quad2xyz(a,b,c,d)
            x =  1/root2 * (a - b - c + d)
            y =  1/root2 * (a - b + c - d)
            z =  1/root2 * (a + b - c - d)
    endproc

    procedure xyz2quad(x,y,z)
            q(1) = 1/root2 * (iif(x>=0,x, 0)+iif(y>=0,y, 0)+iif(z>=0,z, 0))
            q(2) = 1/root2 * (iif(x>=0,0,-x)+iif(y>=0,0,-y)+iif(z>=0,z, 0))
            q(3) = 1/root2 * (iif(x>=0,0,-x)+iif(y>=0,y, 0)+iif(z>=0,0,-z))
            q(4) = 1/root2 * (iif(x>=0,x, 0)+iif(y>=0,0,-y)+iif(z>=0,0,-z))
            simplify( )
    endproc

    procedure simplify
            local i
            minval=q(1)
            for i=1 to 4
                minval = min(minval,q(i))
            endfor
            for i=1 to 4
                q(i)=q(i)-minval
            endfor
    endproc

Additional readings and resources:

• An Introduction to Quadrays
• Source code for a 4D turtle (in VFP 5.0)
• Downloadable XYZ-Quadrays worksheet (Mathcad 6.0)
• Random Walk Trials an IVM
• Pascal's Tetrahedron and T-Space
• Gerald de Jong's Genome applet