|
Bob Burton, The OSU math prof facilitating the break-out session
asked me for a specific example of what the standard curriculum is
leaving out (he wondered if our math head speakers were more a
"last gasp of the Renaissance?" -- something I squeek-wrote on the
flip-chart as a good leading question), at which point I inserted a
plug for my afternoon session. "Come to Beyond Flatland and
I'll give you all the ammo you need" I announced -- earlier I
suggested we all use the internet to better organize and stay in
touch between summits, after hours if necessary (lots of nods).
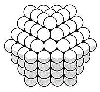 I started my talk
off with ClockTet
by Richard Hawkins (in association with myself),
a four minute computer animation with the clock face as a central metaphor.
I told the class I'd show it again at the end, and they could measure
their increased appreciation for its content by the new insights they'd
have on second viewing -- "an easy kind of test". Then I got my 31 slides-on-tape
rolling, 18 seconds per shot, running through three topics: Concentric
Hierarchy, Sphere Packing and Frequency.
I emphasized that most of this material was in the public domain, on
the internet, and if their school had invested in a digital camera,
they could duplicate my process for creating such slide shows (the handout
gave more details). Then I went to the overheads and went over these
same topics in more detail, every so often picking up a physical model
(before class, as people were taking their seats, I passed a bunch of
models around, including Russell's high tech tensegrity
coupler, plus some museum gift shop stuff) and going over the basic
principles. I started my talk
off with ClockTet
by Richard Hawkins (in association with myself),
a four minute computer animation with the clock face as a central metaphor.
I told the class I'd show it again at the end, and they could measure
their increased appreciation for its content by the new insights they'd
have on second viewing -- "an easy kind of test". Then I got my 31 slides-on-tape
rolling, 18 seconds per shot, running through three topics: Concentric
Hierarchy, Sphere Packing and Frequency.
I emphasized that most of this material was in the public domain, on
the internet, and if their school had invested in a digital camera,
they could duplicate my process for creating such slide shows (the handout
gave more details). Then I went to the overheads and went over these
same topics in more detail, every so often picking up a physical model
(before class, as people were taking their seats, I passed a bunch of
models around, including Russell's high tech tensegrity
coupler, plus some museum gift shop stuff) and going over the basic
principles.
|
|
Ralph told the teachers that more conservative minds, some of whom
he much respected, had originally tried too hard to control chaos,
like through the Office of Naval Research, narrowing its band of
operations to something minimal and controllable. He offered this
as an analogy as to what might be going on in Oregon around
standards testing -- too much rigidity in the face of inherently
dynamical systems. Then he launched into a brief explication of
what dynamical systems theory is all about (strong links to the
calculus), getting around to his teaching in chronological sequence
ideas.
I asked if maybe the chronological approach meant we should do
more to present mathematics as a discontinuous zig zaggy evolution,
with lots of dead ends and withering branches -- more like the
Kuhnian analysis of science's checkered past, with all those
upsetting paradigm shifts and oldsters going down with their ships
and so on (that metaphor comes to me now -- didn't use it then, but
did mention Kuhn). And wouldn't this involve studying "the
heresies" -- like I'd just been reading
Bishop Berkeley's problems with '1/infinity' as used to prove
stuff in the calculus -- people said they'd addressed his concerns
after he died, but I thought he'd still be objecting today.
"Mathematicians could sometimes be really mean dudes" I went on
(thinking of those brutal dueling episodes, although the two such
episodes I recall were with non-mathematicians) and math involves a
lot of arguing, polemics, games with funding (like look what
Kronecker did to
Weierstrass and
Cantor) -- shouldn't we share this with kids, instead of
presenting the subject as a cold "everyone agrees" type thing?
Ralph heartily agreed (he knows first hand what it means to wage an
up-hill battle).
I also mentioned I thought the chaos people had a PR problem, in
that the general public immediately thinks of fractals and
recursive self-similarity, but Ralph hadn't mentioned those at all.
He agreed, and traced the problem to Gleick's book, which went
heavily for fractals because of all the pretty pictures. He didn't
begrudge James Gleick his
million-dollar success with that book Chaos, acknowledging a
narrow overlap of chaos theory with fractals in the region of
strange attractors, but felt the general public had somewhat the
wrong idea as a result (like, so what else is new when it comes to
the general public, right?).
The evening Penrose talk was open to the general public (for a
fee) with front rows roped off for us teachers and presenters. I
got there early and bummed some bucks from Terry when he came in
with Sir Penrose, so I could get some gas for the Subaru (and a Big
Mac as it turned out). Maggie Niess, OSU science-math ed
chairperson and conference organizer (along with her secretary
Rose) said she was sorry about the dinner snafu (I shrugged it
off). Ralph took a front row seat across the aisle from me and we
settled in to listen to Penrose do his thing.
 Sir
Penrose has added the "tribar" as something for which he and his
father should be remembered. That's that "impossible triangle" used
in those famous Escher lithographs as a basis of the forever
ascending staircase and descending waterfall. The toilet paper
royalties infringement was also mentioned by OSU President Paul
Risser as a part of his introduction, plus we all applauded state
education head Norma Paulus for making the Math Summit a reality --
thanks in part to Terry's connections (my wife Dawn is the ISEPP
bookkeeper, and she was quick to suggest I would be a relevant
presenter at this event, and Terry immediately agreed -- really
quick thinking on her part). Sir
Penrose has added the "tribar" as something for which he and his
father should be remembered. That's that "impossible triangle" used
in those famous Escher lithographs as a basis of the forever
ascending staircase and descending waterfall. The toilet paper
royalties infringement was also mentioned by OSU President Paul
Risser as a part of his introduction, plus we all applauded state
education head Norma Paulus for making the Math Summit a reality --
thanks in part to Terry's connections (my wife Dawn is the ISEPP
bookkeeper, and she was quick to suggest I would be a relevant
presenter at this event, and Terry immediately agreed -- really
quick thinking on her part).
Penrose is looking for physical phenomena of a sufficiently
noncomputable nature to serve as an anchor for our mental world,
wherein we have access to the Platonic realm (via mathematics
especially). He emphasizes that computers don't have access to the
Platonic realm, because they simply follow rules whereas although
humans accept rules, and recognize new truths as consistent with
them, they then proceed to transcend them by accessing truths the
rules simply don't predict or anticipate. I was thinking of Kant's
"synthetic a priori judgements" and Stuart
Kaufmann's synergetic "exaptations" as relevant in this
connection.
To prove how computers can be trapped into revealing their
innate stupidity by their own rule-following limitations, he had
some chess problems which show at a glance how white can force a
draw, but which computers, including Deep Thought and Deep Blue,
all bungle, by taking the rook as bait, breaking the wall of pawns
that is clearly the white king's only defense. He went on to
discuss other brilliant insights that mathematicians have had
(proof of their transcendent access to the Platonic realm) which
leave computers in the dust, as far as manifesting any creative
intelligence is concerned.
So where in the brain do we localize the phenomena which make
humans so special vis-a-vis their robot analogues? The title of the
talk was The Large, The Small and the Human Mind -- also the
title of the upcoming book. The idea here is that we have fairly
clear and deterministic models of the very large and the very
small, but they don't converge in mediophase very successfully,
suggesting some new physics is needed, which will incorporate the
human mind as a bridging phenomenon. The new physics will replace
the conventional view that quantum mechanics goes to probabilities
in mediophase, suggesting instead that it goes to certainties in
short time frames with quantum gravity perhaps explaining what
forces the wave function to collapse, leaving the cat dead or
alive, not in some superpositional quasi-state.
Penrose is focusing on microtubes in the neurons as possibly
sensitively constructed enough to register superpositions of
quantum states for very short time periods, thereby allowing human
consciousness make use of quantum entanglements to escape any rigid
determinism and to make these leaps to higher Platonic levels even
while still remaining brain-embedded in the physical world -- as
are the stupid computers. The difference between brains and
computers is that brains are sensitive enough to register the
effects of quantum gravity (whatever "gravity" is -- and whatever
"awareness" is, a key term Penrose was reluctant to define, but
which he suggested we all know from experience).
Although he mentioned philosophy as feeding into this talk in
places, Penrose made it clear that mathematics and physics were his
focus areas. My question was clearly coming out of the philosophy
department however -- at the end I quoted
Wittgenstein saying something like "if 'consciousness' has any
meaning, it must be a humble one, like 'table' 'lamp' or 'chair'."
I said I understood from his presentation of Gödel that we
could keep enlarging the sphere of truth, consistently with
accepted rules (i.e. without breaking any) but in ways not
predicted by them either (thinking of Kaufmann again, though I
didn't try to stuff his "exaptations" into my question). Now that
physics was feeling ambitious enough to absorb "consciouness" as
another one of its key terms, I wondered if maybe the evolving
usage patterns were changing its meaning, such that "consciousness"
out the other end of the Penrose syllabus had a different "spin"
than it had going in -- a sort of moving target in other words, "a
kind of zero."
Penrose didn't agree of course, as he sees consciousness as an
objective, static thing which we all experience through qualia and
experiences of emotion and understanding and so on -- a view shared
by the general public by and large. The goal is to discover its
physical basis while consciousness itself "holds still" as we solve
the surrounding puzzles. By analogy I suggested that if Newton
returned he'd need some considerable reschooling to catch up on
what we mean by "gravity" in this day and age (e.g. all that "shape
of spacetime" stuff) and again Penrose disagreed, seeing "gravity"
as a fixed point of reference as familiarly Newton's today as ever.
Obviously my view that key terms have wordmeaning trajectories
within fields created from usage patterns, and do not map to
reality as representational so much as operate within it as
codefinitional, is not one with which Penrose feels
comfortable.
I introduced my question by saying I would then follow Terry's
suggestion and run the cordless mike to others in the audience
wishing to ask questions, and this I proceeded to do, although some
had such booming voices I judged no amplification necessary.
Audience questions focused on whether our orderly and comprehending
awareness were really evidence of access to a Platonic realm or
more a reflection of physical principles embedded in the design of
nature, and hence the brain. Perhaps our intelligence is of local
views only, with a greater universe not penetrating our thick
skulls, because of no survival value (this from an Asian gentleman
with a thick accent -- Penrose seemed to have a hard time with it).
Towards the end of the Q&A Penrose willingly superimposed his
three worlds (physical, mental and Platonic), apparently
acknowledging that the mysteries associated with their
interrelationships were perhaps collapsible into a single mystery
of being.
People seemed honestly intrigued and engaged by the talk,
although of course a lot of it went right over our heads (Ralph
seemed to be nodding off in a few places I noticed, but laughed at
the cartoon Penrose projected, which showed how nature probably
doesn't select for pure mathematicians, the early human kneeling in
the dust with his gizmos, oblivious to his surroundings, being
almost certain tiger-bait, compared to his compatriots busy doing
more "useful and meaningful" applied technology type things).
I bought some gas (Arco) for the Subaru and and a Big Mac
(Mickey D's) for me and headed north to Portland on 99W, arriving
home after midnight, and falling into my dreamworld while reading
Feynman's introduction to QED.
For further reading:
|
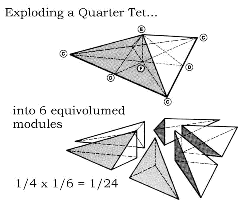




 I started my talk
off with
I started my talk
off with 
 Sir
Penrose has added the "tribar" as something for which he and his
father should be remembered. That's that "impossible triangle" used
in those famous Escher lithographs as a basis of the forever
ascending staircase and descending waterfall. The toilet paper
royalties infringement was also mentioned by OSU President Paul
Risser as a part of his introduction, plus we all applauded state
education head Norma Paulus for making the Math Summit a reality --
thanks in part to Terry's connections (my wife
Sir
Penrose has added the "tribar" as something for which he and his
father should be remembered. That's that "impossible triangle" used
in those famous Escher lithographs as a basis of the forever
ascending staircase and descending waterfall. The toilet paper
royalties infringement was also mentioned by OSU President Paul
Risser as a part of his introduction, plus we all applauded state
education head Norma Paulus for making the Math Summit a reality --
thanks in part to Terry's connections (my wife