Quantum Modules

Quantum may be used in the sense of "fundamental unit or increment." In synergetics, polyhedra analyze into fundamental increments of volume known as quantum modules, or mods for short. The A and B mods derive from the regular tetrahedron and octahedron respectively. The tetrahedron consists of 24 A modules, 12 left handed and 12 right handed (or, alternatively, 12 inside out and 12 outside out -- inside-outing being another way of changing handedness, a left handed glove being an inside out right handed glove).

A Module

A-mod (1/24 tetrahedron) by [rh]

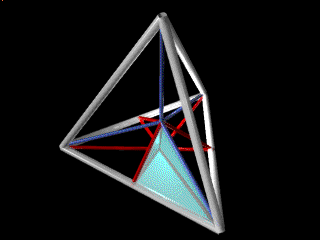24 A modules comprise the regular tetrahedron. As the latter is ascribed a volume of 1, each A-mod has a volume of 1/24.

B Module

B-mod (1/96th octahedron) by [rh]

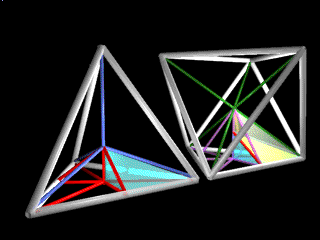The regular octahedron is comprised of 48 A mods and 48 B mods. Since A and B mods have equal volume, the total volume of the octahedron is 4 (96 times 1/24). Other polyhedra in the synergetic hierarchy, excepting those of 5-fold symmetry, may also be assembled from combinations of A and B modules.

MITE

MITE (1/8 tetrahedron) by [rh]

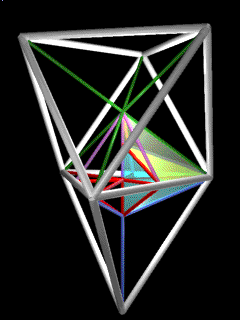An irregular tetrahedron comprised of 2 A's and 1 B, known as the MITE (minumum tetrahedron) is the simplest -- in terms of fewest edges etc. -- space filler. Left and right handed MITEs are outwardly identical. 8 MITEs assemble the space-filling, unit-volume Coupler (see below), an irregular octahedron formed by connecting the centers of face-bonded, space-filling rhombic dodecahedra. 24 MITEs assemble the cube.

Coupler

Coupler (volume=1) by [rh]

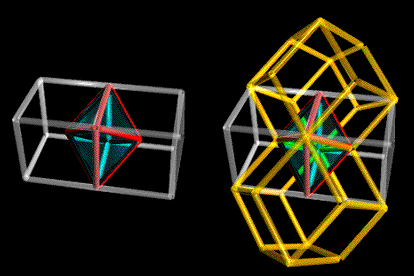Space-filling cubes also define Couplers. Their common square faces define longitudinal slices through these irregular octahedra, creating half-couplers or Kites (volume 1/2). Individual cubes are comprised of 6 such half-couplers, for a volume of 3. The half-couplers defined by rhombic dodecahedra are sliced along an axis perpendicular to the cube-face cuts. Twelve such half-couplers make up the space-filling rhombic dodecahedron (volume 6).

At his SpringSpace website, Karl Erickson explores A and B mods, MITEs and Couplers, by means of Gerald de Jong's StruckJava, an interactive geometry applet based on the concept of 'elastic intervals' or 'springs'.

The topic of modules links to a broad range of historical and contemporary investigations, both internally and externally to Synergetics. For example, David Koski has developed an elegant set of modules for constructing shapes having five-fold symmetry, which the A and B mods cannot encompass. Koski begins by carving up the 'golden cuboid', a brick-shaped volume of edges phi, 1 and 1/phi. The resulting tetrahedra (one of which is the same shape as the Synergetics T mod though differently scaled), comprise the basic templates, and may find their linear dimensions rescaled by powers of phi when participating in various five-fold symmetric assemblies.

Yasushi Kajikawa has innovated an alternative approach to modularizing the five-fold world, using three edge lengths to construct his ten template shapes.

These explorations link to those of Roger Penrose and many others.

For further reading:

1. A & B module hypertoons (Quicktime) by Richard Hawkins
2. Concentric Hierarchy
3. Quadrays and Volume
4. More re Koski's modules posted to geometry-research the Math Forum ( plus erratum)
5. Foldable patterns for the A & B modules
6. Re: A and B modules as per R. Williams and R.B. Fuller
7. Some T-module calculations

Graphics by Richard Hawkins [rh] using Alias Animator V5.1 on an SGI Indigo2 Extreme