Quadrays and Volume
by Kirby Urner
First posted: November 9, 1997
Last updated: February 23, 2000
Any tetrahedron may be represented in terms of rays to its four
vertices originating from some common point. For example, in the
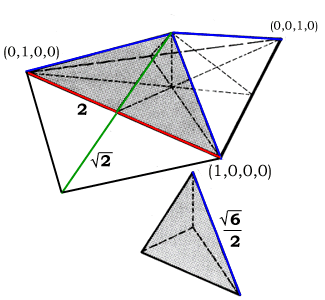
case of the regular tetrahedron, we can simply use the quadray
basis set: (1,0,0,0) (0,1,0,0) (0,0,1,0) (0,0,0,1). Unless the
origin itself is a vertex, the tetrahedron's set of six
edges will not include any of the four vertex-defining vectors.
Counting (0,0,0,0) as a zero-vector, we can always net the
tetrahedron's edges as six vector subtractions representing the
differences between pairs of vertices.
For example, as we learned in An Introduction to Quadrays, the edge between (1,0,0,0) and (0,1,0,0) has a length and direction given by: (1,0,0,0) - (0,1,0,0) = (2,0,1,1). We could also write this difference as (0,1,0,0) - (1,0,0,0) which gives (0,2,1,1), a vector pointing in the opposite direction. However, since this is paper about volume, it is a vector's length, and not its positive versus negative directionality, which proves relevant in our calculations.

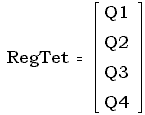
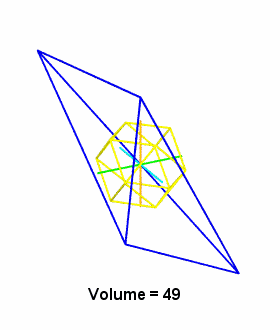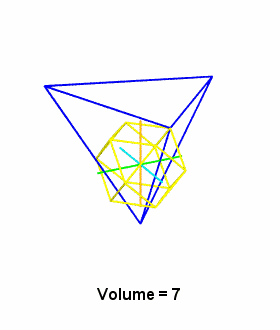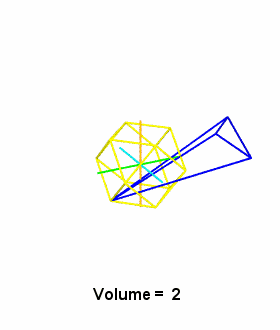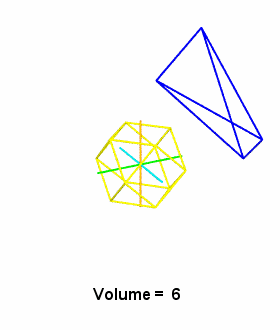
For convenience, we can store the four vectors in a matrix, where each row represents a vertex. We can then feed a special case matrix to our volume function, a method defined within our generic tetrahedron class.
Our class method for operating on such a matrix comes from Gerald de Jong. Although aware that Leonhard Euler had come up with an expression for the tetrahedron's volume, given only its six edge lengths as input, Gerald resolved to derive such an expression independently.
Gerald's elegant result, which relates the algebraic terms to open and closed triangles, and opposite edge pairs, made its first public appearance in the form of a Java applet, subsequently modified to accommodate the synergetics approach, which takes our regular "home base" quadray tetrahedron as its unit of volume.