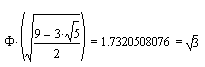Quadrays and
the Concentric Hierarchy

Our goal in this paper is to use quadrays to create ray tracings of some of the shapes making up the synergetics concentric hierarchy.

The strategy employed centers around two lookup tables in a relational database: a table of points (allpoints) and a table of edges connecting pairs of points (shapes). Every shape is defined as a set of edges (polyhedra treated as wireframes), and each edge is defined as a point pair.

Our points are defined using 4-tuples (a,b,c,d). For example, the four corners of the starting tetrahedron are defined as (1,0,0,0) (0,1,0,0) (0,0,1,0) and (0,0,0,1) and its edges consists of all possible pairs of corners -- six in all.

If we identify the corners of tetrahedron T1 as T1A through T1D, then the edges will be:

(T1A,T1B) (T1A,T1C) (T1A,T1D) 
(T1B,T1C) (T1B,T1D) (T1C,T1D)

The negatives of our original four points define the corners of the dual tetrahedron, one intersecting the original at its mid-edges. In quadray notation, to negate a vector is to get one pointing in the opposite direction, just as we would expect from our experience with the xyz coordinate system. However, we learned an An Introduction to Quadrays that only positive numbers are required to specify all vectors in quadray space. For example, -(1,0,0,0) = (-1,0,0,0) = (0,1,1,1).

Below we see the original tetrahedron T1, its dual T2, and the two tetrahedra interpenetrating one another (T1+T2):

In the concentric hierarchy, each of the above tetrahedra has unit volume. Taken together, they consist of one whole unit-volume tetrahedron with four protrusions of 1/2 the original edge and therefore with a volume of 1/8 apiece: 1 + 4/8 = 1.5.

The tetrahedron and its dual also define the eight corners of a cube. In our shapes table, we define cube C1 as pairs of points already defined in association with T1 and T2. In other words, we don't need to add any new points to our database, just more edges.

Below we see a listing of all records in the shapes table defining our concentric hierarchy cube of volume 3. The program scans through these records and builds lines of text using syntax which the ray tracing program, Povray, knows how to interpret as a colored cylinder running from point ID1 to point ID2. Tiny spheres are defined at each end to give our cylinders rounded ends.

  SHAPEID      ID1      ID2     
  -------------------------
  C1           T1A      T2B     
  C1           T1A      T2C     
  C1           T1A      T2D     
  C1           T1B      T2A     
  C1           T1B      T2C     
  C1           T1B      T2D     
  C1           T1C      T2A     
  C1           T1C      T2B     
  C1           T1C      T2D     
  C1           T1D      T2A     
  C1           T1D      T2B     
  C1           T1D      T2C     

To bring the octahedron into the picture, we need more points as well as more edges (point pairs). The octahedron is the cube's dual, meaning its edges are perpendicular to the cube's. In the concentric hierachy, the octahedron has a volume of 4. One way to see this is to realize that the smaller octahedron shared by the two intersecting unit-volume tetrahedra has a volume of 1-1/2 or 1/2. This new octahedron has edges twice as long and therefore 8 times the volume: 8 x 1/2 = 4.

Moving on to the rhombic dodecahedron of volume 6, we are once again faced with a situation of needing only to connect already existing points. The cube and the octahedron together define the 12 rhombic faces, their edges intersecting at 90 degrees at each rhombus face center. So our shapes table need only be augmented with edges connecting each octahedron vertex to the four neighboring cube vertices. This adds 24 new edges to shapes, but nothing to allpoints.

Recall that the rhombic dodecahedron is the domain of a unit-radius sphere. Dense-packed IVM spheres intertouch at kissing points at the centers of the rhombic faces. This presents us with an opportunity to experiment with Povray's many texturing and colorizing options. The following additional text generated the dark, woody unit-radius sphere at the center.

sphere { <0, 0, 0>, 1
    texture {
      pigment {
        wood
        color_map {
          [0.0 color DarkTan]
          [0.9 color DarkBrown]
          [1.0 color VeryDarkBrown]
        }
        turbulence 0.08
      }
      finish { phong .5 }
    }
  }

We are now ready to surround our rhombic dodecahedron with the cuboctahedron of volume 20. This shape is defined by the 12 centers of the unit-radius spheres packing around a nuclear sphere. It is also the dual of the rhombic dodecahedron, although this time we're not scaling it to intersect its dual at mid-edge points. Its 24 edges are equal in length to the unit-volume tetrahedron's, and as such internally subdivides into 8 tetrahedra and 6 half octahedra: 8 + 6 x 2 = 20.

Notice that rhombic dodecahedron vertices occur at the centers of the cuboctahedron's square faces. These are equivalently the termini of the octahedron of volume 4, which is embedded in the rhombic dodecahedron as a set of 12 long diagonals.

The shapes we have defined so far are all 3,4-fold symmetric, may be assembled from A and B modules and have whole number volumes relative to the unit-volume tetrahedron. The 5-fold symmetric members of the hierarchy, by contrast, have incommensurable volumes (or incommensurable edge lengths) . The Jitterbug Transformation serves as a bridge between the two symmetry families in synergetics, by taking the cuboctahedron through an icosahedral phase enroute to becoming an octahedron.

Starting with the cuboctahedron, we note that its 6 square diagonals have a length of 2 x root(2), given circumferential vectors of 2. Note that these diagonals come as 3 pairs of parallel segments, likewise 2 x root(2) apart. In going to the icosahedron, these diagonals get pushed further from their common center and shortened, without disturbing the parallel relationships.

Because the 3 original pairs are oriented in the mutually perpendicular xyz directions, the pushing apart and the shortening involve moving existing points in the xyz directions. Expressed as quadrays, these xyz directions are:

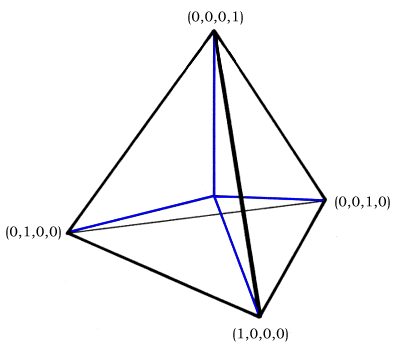
(0,0,1,1) (0,1,0,1) (0,0,1,1)
(1,0,0,1) (1,0,1,0) (1,1,0,0)

So our pushing apart and shortening operations involves adding vectors in the above six directions, after first scaling them by precise amounts. Scaling involves first dividing a vector by its native distance, such as root(2) in the case of the above 6, which effectively makes it unit length. Given our turtle objects internally track a vector's distance, scaling to unity is easy to implement. Then whatever additional scaling factors are applied.

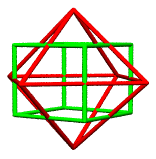
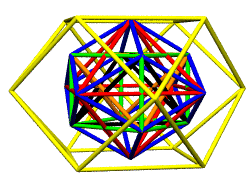
The scaled and added vectors will move existing vertices of the cuboctahedron out and closer together, to give 3 golden rectangles, with external edges of 1, and cross beams -- through the interior of the cuboctahedron -- of length 2 x phi (where phi = [1 + root(5)]/2)

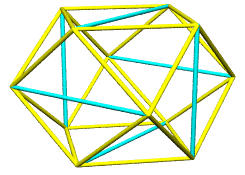
The initial cuboctahedron vertices are at the locations:

(0,1,1,2) (0,1,2,1) (0,2,1,1)
(1,0,1,2) (1,0,2,1) (1,1,0,2)
(1,1,2,0) (1,2,0,1) (1,2,1,0)
(2,0,1,1) (2,1,0,1) (2,1,1,0)

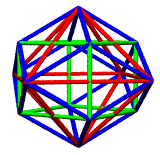
These quadray vector additions generate 12 new points for the allpoints table, and 30 new entries in shapes, patterned after those used for V1 + VS (cuboctahedron plus 6 square diagonals). Given the new data for I1, the existing makeshape( ) method provides the expected icosahedron of volume ~18.51.

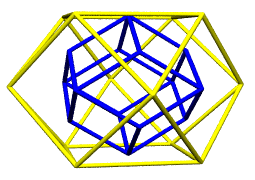
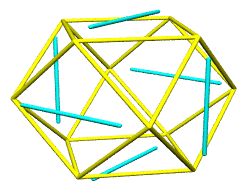
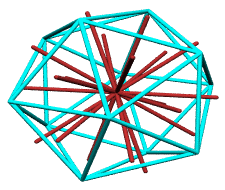
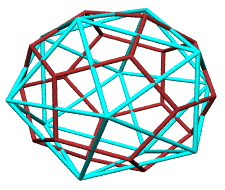
We develop the pentagonal dodecahedron by adding the 3 quadrays associated with each of the icosahedron's 20 triangles. Each 3-vector sum provides a spoke aimed straight through an icosahedron face center. A scale factor of 1/distance shortens the spokes to unit length, and a second scale factor extends them to provide a dodecahedron with mid-edges perpendicalar to and intersecting the icosahedron's. This second scale factor was computed using Figure 986.405 and Figure 986.411A in Synergetics (2nd volume) and is:

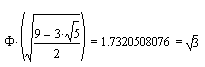
This pentagonal dodecahedron, the icosahedron's dual, supplies the remaining vertices of the rhombic triacontahedron, another five-fold symmetric member of the synergetics concentric hierarchy.

In Fuller's paradigm, the rhombic triacontahedron is scaled either of two ways:

• As 120 T modules of volume 1/24 each, the same volume as the A and B modules, but with a radius of ~0.9995
• As 120 E modules of slightly greater volume, and with a body-center to rhombic face-center radius of precisely 1

As a practical matter, our ray tracing program will not be able to visually convey the miniscule difference in scale between these two shapes. For convenience, the E modular version will be calculated and stored.

At left above we see the icosahedron and pentagonal dodecahedron serving as a framework for the 60 additional edges of the rhombic triacontahedron of radius phi (center to mid-face). Beneath is a rescaled rhombic triacontahedron of radius 1, obtained by multiplying its edges by a factor of 1/phi. The original cuboctahedron and icosahedron are provided as context.

Note that this E-modular rhombic triacontahedron of volume 5+, like the rhombic dodecahedron of volume 6, has face centers tangent to the inscribed unit-radius sphere, as shown at right.

This essentially completes our study of the concentric hierarchy using quadrays. A cuboctahedron of volume 2.5 (inscribed in the volume 3 cube) and a cube of volume 24 (in which the volume 20 cuboctahedron is inscribed) also play a role in Synergetics. And of course the A, B, T and E modules deserve further analysis in terms of quadrays.

As a grand finale, its worth superimposing all of the discussed shapes, although this makes for a rather "busy" picture...

For further reading:

• Tabular data used in this study (some of it)
• Source code used in this study
• Volumes in Synergetics
• Quadrays and Volume
• Introduction to Synergetics
• An Introduction to Quadrays