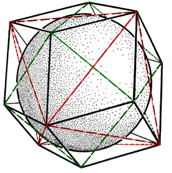
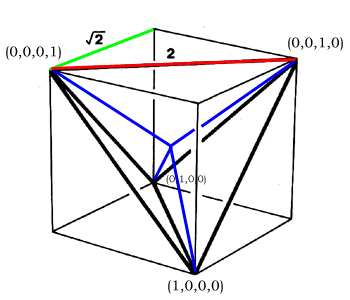
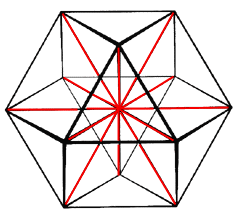
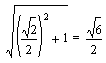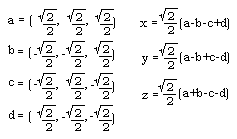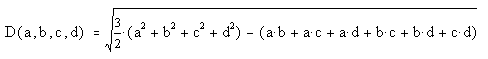| The above distance function operates on quadrays
regardless of how they're nomalized. However, sometimes if we get
more specific about the form of normalization, we can simplify our
quadray expressions considerably. Let's examine how this works in
this case of a distance formula.
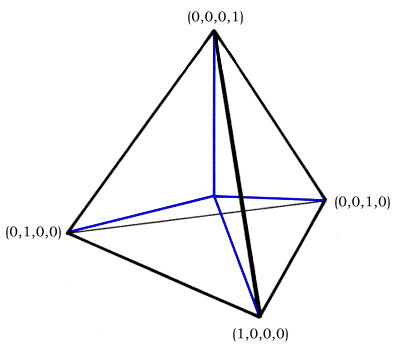
Because any (k,k,k,k) denotes four quadrays pointing equally in
the four basic directions, it serves as an "additive identity" i.e.
(k,k,k,k) may be added to any quadray without changing its
direction or magnitude.
Given this freedom to add any (k,k,k,k) to any quadray without
changing it, we have the option to normalize quadrays according to
a variety of rules.
For example, we can require that a+b+c+d=0 for any quadray
(a,b,c,d), and get there by adding some (k,k,k,k). Simply set the
value of k to -(a+b+c+d)/4 in this case.
Tom Ace
came up with the above method for "normalizing to zero" in the
process of deriving an alternative, and much less complicated
expression for the length of a quadray. His expression for
distance, using this "zero-based" format, is simply:
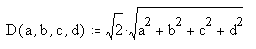
where the root(2) multiplier in front scales the
result in accordance with the stipulation that our "home base"
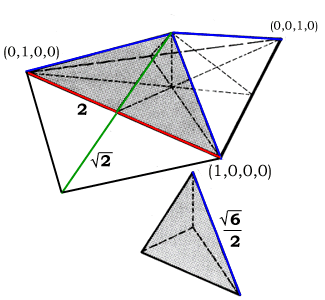
tetrahedron should have edges = 2 (and consequently D(1,0,0,0) =
root(6)/2).
Note that we might want to express our vector
lengths using IVM sphere diameters as units, or the basis
quadrays themselves. In other words, if our quadray tetrahedron is
defined to have unit edges, such that IVM sphere radii are valued
at 1/2, then we will use different constants in our distance and
quadray-to-XYZ conversion formulae. Likewise, we might choose to
define D(1,0,0,0)=1, in which case the tetrahedron's edges will
need to be multiplied accordingly.
To prevent confusion, it may help to think in terms
of units like feet and inches. The exact form of our expressions
depends on whether we want to use R, D or Q (quadray) as our units
of measure. In this introductory essay, I use R units.
Elsewhere, I have used D units.
Other authors have used Q units.
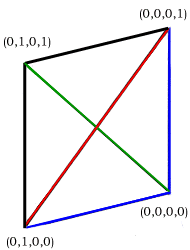
These alternative zero- or one-based normalizations
may well feature a negative operator, as in
-(1,0,0,0). Geometrically speaking, the negatives of the
four basis quadrays correspond to the quadrays of the "inverse
tetrahedron", which point outward from (0,0,0,0) at 180 degrees to
those of the "home base" or "all positive" tetrahedron.
As demonstrated above, negative numbers are
perfectly meaningful within quadray 4-tuples, but we always have
the option to renormalize such that they go away, if we so
desire.
|