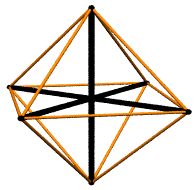
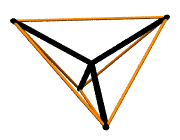
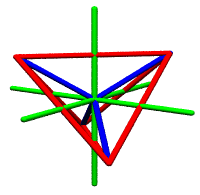
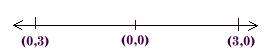Investigations into
the Linear Algebra Concepts
used in the XYZ and
Quadray Language Games

by Kirby Urner

First posted: November 20, 1997
Last updated: October 1, 2005

The quadray basis vectors go to the corners of a regular tetrahedron from the origin at (0,0,0,0). They're basis vectors in the sense that no three algebraically add to give the fourth using the closed, canonical notation suggested in many texts: no negative numbers, at least one of the four coordinates zero.

What is true is at least one basis vector is always not needed for any given point, whereas Cartesians posit three mutually orthogonal numberlines in R**3 (Python notation) and require the involvement of each for all points but those directly on the axes.

However, if we count positive and negative rays separately, per the quadray practice (we'll get to negatives in a moment), then the Cartesian actually has six basis vectors, not three.

The question is how do we treat the operation of reversing direction -- should this be considered a form of scaling (e.g. multiplication by -1), or another operation in its own right, i.e. that of negation.

 

 6SPOKES.gif - 7.2 K
4SPOKES.gif - 4.1 K
Scalar multiplication is something of a hybrid concept, because it includes what might be considered entirely separable operations: scaling a vector (expanding or contracting it) without changing its orientation, versus rotating a vector by 180 degrees, which is what the negative sign accomplishes if the scalar is negatively valued.

What quadrays permit is something xyz does not: 4-tuple addresses consisting entirely of one sign (either positive or negative). Even if we normalize by some other scheme, such as to make the sum of the coordinates (a,b,c,d) equal zero, or one, we always have access to an all-same-sign 4-tuple isomorphism. This means we can afford to take only the first notion of scaling (expanding and contracting) and let go of the second (180 degree reversal) and still use vector addition to span volume.
So our quadray vectors might be considered basis vectors if we adopt a notion of "strict" scaling. Whereas the three xyz basis vectors, i,j and k, will not natively add to reach points outside of their all-positive octant without scaling of the vector reversal type (negation), quadrays natively will.

This stricter definition of scalar multiplication doesn't preclude having the negative operator in the picture, but it does suggest in what sense we might define the quadrays (1,0,0,0) (0,1,0,0) (0,0,1,0) and (0,0,0,1) as "basis vectors": in combination with our "strict" definition of scaling. Negation, or vector reversal, is by this definition considered a separate (though of course still doable) operation.

 Q1X1.gif - 6.5 K
In sum, the xyz game needs two operations: vector grow/shrink and vector reversal, in support of tip-to-tail vector addition, in order to reach all points, whereas the quadray game only needs the grow/shrink operation, and not vector reversal, to have vector addition perform adequately.

Because we habitually associate number or magnitude with length or distance in any number of contexts, including that of the "real number line", it is perhaps somewhat more problematic to separate our concepts of "scalar" and "vector" than the linear algebra text books would have us believe.

Adapting the quadrays notation to the number line, we might use coordinate pairs in place of signage, i.e. write (0,3) in place of -3, and (3,0) in place of +3. Then we might then write |(0,3)| = |(3,0)| = 3, meaning the absolute value of these two entities is the same, but is not geometrically equivalent to either one.
image
But then isn't absolute value generally considered a length or distance? Absolutely. Therefore its representation takes us back to the number line, where it becomes congruent with +3 -- or (3,0) -- but never with -3, or (0,3). But why is one side of zero favored as the location for "absolutes", while the other side is not?

(0,3) and (3,0) look a lot more like vectors, notationally speaking, than do -3 and +3, especially in light of the fact that we don't usually write +3, but 3 -- the same symbol we use for the value of |-3|. In ordinary notation, it looks like 3 is its own absolute value, but that -3 isn't "absolute" in the same way. This asymmetry carries over into the language of linear algebra, wherein only the positive xyz vectors (1,0,0) (0,1,0) (0,0,1) are the "basis" vectors, even though mirror images of these vectors do the same work.

Quadrays provide an opportunity to study all these design issues regarding the geometric interpretation of our symbolic processes (and vice versa). They provide useful contrast with xyz in the sense that they don't require these two different "kinds" of scalar multiplication (the length-changing kind and the orientation-changing kind) and thereby give us a sense of what it's like to not have "negative mirroring" operative in quite the same way.

The interface between numbers and geometry is only simple and straightforward at first glance. Once you start to investigate this interface more deeply, many issues arise for consideration -- as do the recorded thoughts of many thinkers who have wrestled with these very questions. Linear algebra as a discipline is one of the more historically recent attempts to formalize and codify this interface.

If we agree that the quadrays apparatus consists of four "basis vectors" which span volume when abetted with strict scaling and vector addition, then we come up against the concept of "dimension", which in linear algebra is always identified with the number of basis vectors necessary to span a vector space.

Shall we say that "volume is 4D" then?

Given this is the same volume mapped by xyz, the one we all learn fairly early on is "3D", such an alternative nomenclature is unlikely to stand much chance of widespread adoption. However, this usage of "4D" is consistent with the writings of at least one mathematically-inclined philosopher, namely those of R. Buckminster Fuller, author of Synergetics: Explorations in the Geometry of Thinking. So at least one (albiet highly specialized) application of the quadrays "language game" has so far emerged within our shared curriculum context. Perhaps others will follow.

For further reading:

Synergetics on the Web
maintained by Kirby Urner