Pascal's Tetrahedron
& T-space [1]

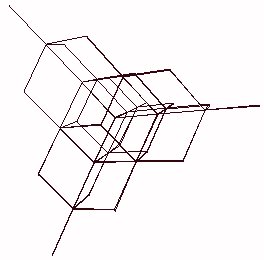
You drop a bead through the apex of a tetrahedron, it falls straight down to the center, where it encounters three branching pipes, each to a base vertex. Each vertex is then the apex of yet another tetrahedron, and so on down. This is Pascal's Tetrahedron (Brian Hutchings shares the marquee as per postings to Synergetics-L).

This is also the fanning out of T-paths, where returning up against gravity is not an option. (1,0,0,0) (0,1,0,0) and (0,0,1,0) are your only options (0,0,0,1) being defined as upward in this picture.

You do fall down however, so the (0,0,0,1) path gets used, in reverse. Dare we invite (0,0,0,-1) into the picture? This is equivalently (1,1,1,0). So after each roll down a slanted pipe, we'll need a straight-down fall along (1,1,1,0) to complete the picture. We should start with such a fall as well, down to the first decision point.

Note that in constructing this apparatus from T-paths, we are imposing a different regime than the v-rays by themselves. The T-path matrix as described by v-rays alone (no other restrictions) is one of face-bonded hexahedra of volume 1.5, four around a common vertex giving a rhombic dodecahedron of volume 6.

The positive and negative T-path lattices, superimposed, outine all the couplers, and therefore we might say:

Although some compact recursive algorithm would get us more unique T-paths with less redundantly visited vertices, and hence a smaller output file, I've already got the randomly walking 4D Logo Turtle strategy, and so get more observable results in less time with something more like the computer program listed below [2].

For those of you with browser-enabled embedded VRML, the output of the random fall algorithm is at right (you'll need to rotate the image to get the 'top' oriented as per the above 'gravity' logic).

Imagine glass cylinders, hexagonally packed, under each exit from the apparatus at bottom. We'd expect a pile of beads in a hill, higher towards the center, sloping down to the edges of the triangle, reaching their lowest at the vertices, each fed by one unique path out of the many T-path options. Instead of a 'bell curve' we might talk about a 'bell hill' with bell curve profiles seen from the sides.

The probability or frequency with which a bead will end up in a given cylinder is given precise numeric expression by the Pascal-method of adding all nodes feeding to a given one (by branch pipe), to give a growing triangle of sums, highest numbers towards the center. These sums count the total number of unique T-paths feeding any given node within our apparatus.

This same counting method may be used in the IVM, with each of the 12 spheres surrounding a nuclear one having a value of 1. At the next level, we start getting Pascal-like aggregates in the 8 tetrahedral and 6 octa- hedral directions. The sums in each sphere would give the number of T-paths to that sphere, along IVM segments only, and stipulating no 'sideways' movment i.e. each hop has to be to a cuboctahedral layer one further outward from the nuclear sphere.

NOTES

[1] David Chako defines T-space as the set of all points reachable by incremental translations in the four v-ray directions (center of a regular tetrahedron to its four vertices), along with the T-paths between them.

These hops are assigned the coordinates (1,0,0,0) (0,1,0,0) (0,0,1,0) and (0,0,0,1) where vector addition is defined e.g. (0,1,1,1) + (1,1,1,0) = (1,2,2,1), along with a simplest form of coordinate address: at least one coordinate zero, all others non-negative e.g.

(3, 2, 1, 1) simplifies to (2, 1, 0, 0)

(0, 0, 0,-1)   -->         (1, 1, 1, 0)

(1, 2, 2, 1)   -->         (0, 1, 1, 0)

For a more detailed and recent investigation of this topic, see my Introduction to Quadrays. Some curriculum writings at the Math Forum give more context for this research into Pascal's Tetrahedron. I also have an essay on the Binomial Theorem featuring Pascal's Triangle.

[2] sample program code

*--------------------

procedure randomwalk4

lparameters depth

* written in Microsoft Visual FoxPro by K. Urner
* (Turtle class source code not shown here)
* this whole procedure gets called 500 times,
* to statistically explore the expanding tree
* of possibilities to a depth of 6

=rand(-1)       && reseed the randomizer

oTurtle.penup()  
oTurtle.setorigin()     && back to the top
oTurtle.pendown()

oTurtle.mov(1,1,1,0)    && drop the bead down the apex

for i=1 to depth
  vdir = mod(int(1+1000*rand()),3)+1  && options 1-3 (not 4)
  oTurtle.movi(vdir)    && indexed movement operator
  oTurtle.mov(1,1,1,0)  && fall straight down to next choice
endfor

oTurtle.writevrml()     && append to the VRML ascii file

return

*--------------------