An Introduction to Synergetics

Synergetics is a self-discipline pioneered by the late R. Buckminster Fuller, who needed a language rooted in first hand experience, trustworthy and comprehensive enough to sustain him through a career involving plenty of heavy duty service on behalf of omnihumanity. He was not the first to shoot for a comprehensivist's viewpoint, and Fuller hoped the results he obtained, with collaborators, including the two Synergetics volumes with E.J. Applewhite, would encourage many more "little me" individuals to likewise go for stellar careers as competent anticipatory design scientists -- or whatever -- this time with the advantage of synergetics to assist them.

Readers of Synergetics may find it works best to approach it as a work in the humanities, as a philosophy, despite the engineering mathematics and geometry it contains. The language is frequently psychological and metaphoric, while many key terms come with an alien spin -- a fact Fuller addresses in Remoteness of Synergetics Vocabulary. This is not a popularization of other people's thinking, but one individual's slant on the whole of Universe -- perhaps inspiring others to likewise roll their own. "Dare to be naive" is the moral of this highly sophisticated piece of literature.

Artists using ray-tracing software describe a scene in terms of its Eulerian topology, before applying various textures. The textures provide visual cues which the viewer interprets as 'solid,' 'liquid' or 'empty space.' When a scene moves from a simple wire-frame to a true landscape, we might think of something abstract becoming 'energized' i.e. becoming reality.

Fuller sought a relationship as general as Euler's for this energetic aspect of reality and thought he found it in the Phase Rule of J. Willard Gibbs. The Phase Rule relates the transformative pathways between the gaseous, liquid and solid phases of chemical components to their ambient temperature and pressure.[1] But synergetics hyperlinks these phases to other more gut-level aspects of experience as well, is designed to resonate with secondary, more alchemical (or psychological) meanings.

Solids, liquids and gases are characterized by different freedoms of relative motion among their constituent molecules: solids hold molecules in relatively fixed arrays, as in crystaline formations; liquids allow currents and flow patterns; gases are comprised of molecules free to move quasi-independently of one-another. Fuller sought to abbreviate these phases using a topological shorthand: face-bonded, edge-bonded and vertex-bonded tetrahedra for solids, liquids and gases respectively. His purpose was to signify an Eulerian aspect to the Phase Rule, thereby unifying Euler and Gibbs into a yet more general formulation of exceptionless principles.[2]

In the topological realm, synergetics does not distinguish between edges, faces and vertices in the way conventionally taught in schools. In 20th century text books, Euclid's vertices, edges and faces, more commonly known as points, lines and planes, have zero, one and two dimensions respectively. Solids have three dimensions and fractals fall somewhere in between -- a fractal might have 1.5 dimensions for example.

Synergetics is a ' geometry of lumps' in which even points occupy volume, however infinitesimal. All objects in synergetic prefrequency topology have the same dimensional characteristics. Nor are 'perfect solids' ever defined. Every surface is permeable. Faces or planes are edge-framed window-openings, not impermeable surfaces. These are differences at the level of definition, with synergetics having the advantage of more hindsight: since Euclid's day: science has shown solid matter to consist mostly of empty space.

Whereas Euclidean space has no boundary, Fullerian conceptual space has a definite shape. The volume with the fewest Eulerian characteristics is the tetrahedron. Six edges meet at four vertices to define four windows. This wire-frame separates an internal from an external region and so defines our concept of volume by giving it a definite shape. Fuller accordingly makes this shape his unit of volume, pointing out its more economical topology vis-a-vis the cube's eight vertices, twelve edges and six framed openings.

Synergetics is therefore a non-Euclidean, non- Cartesian approach to geometry. Its topological primitives are not defined according to the Euclidean template, and its unit of volume is not the cube, nor is its coordinate system xyz, nor is Fullerian space defined to contain infinite volume with no internal or external shape.

Once the regular tetrahedron is posited as a primitive beginning, a more elaborate framework of geometric relationships is defined around it, in the form of a concentric hierarchy of additional polyhedra. The tetrahedron is its own dual, and two interpenetrating tetrahedra comprise the duo-tet cube, with a relative volume of three.

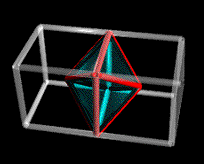The center-point of this cube defines six half-octahedra (irregular) of volume 3/6 or 1/2. These are known as half-couplers in synergetics. Half-couplers face-bonded to the six faces of the cube, mirroring the six internal half-couplers, create a rhombic dodecahedron of volume six. The rhombic dodecahedron is a space-filling shape. When packed together without intervening gaps, the arrangement is coincident with a sphere-packing arrangement familiar to all supermarket grocery clerks and crystallographers.

The rods running between the centers of adjacent space-filling rhombic dodecahedra, equal in length to the edge of our original tetrahedron, describe a skeleton of space-filling tetrahedra (volume 1) and octahedra (volume 4). Each center is connected by twelve rods to twelve adjacent centers. The surrounding centers form the vertices of a cuboctahedron of volume 20 relative to the initial tetrahedron.[3]

And so we have a concentric hierarchy of rationally interelated polyhedra:

Concentric Hierarchy	Polyhedron	Volume
	Tetrahedron	1
	Cube	3
	Octahedron	4
	Rhombic Dodecahedron	6
	Cuboctahedron	20

Synergetics is not a replacement discipline for the many subjects of study, is more designed to augment one's appreciation for the relationships inteconnecting them. Much of the information it contains was already familiar to others, with synergetics simply networking it somewhat differently. In Bucky's case, synergetics served to anchor his thinking around a reference point external to any specific field, in a highly personalized and intuitive space, but without leading to a self-indulgent form of solipsism (on the contrary, he was one of the more outgoing philosophers of all time).

By striving for comprehensivity, synergetics gives its student a means to translate inputs and discoveries from many walks of life into an efficient storage and retrieval system. In this sense, it links up with the memory arts as passed down through the hermetic tradition, is a kind of computer programming language.